Pada UNBK tahun 2018 banyak pemberitaah mengenai Ujian Nasional dari Mulai Matematika ataupun Mata Pelajaran yang lainnya lebih sulit dibandingkan dengan tahun-tahun sebelumnya. Ternyata mulai tahun 2018, Kemendikbud mulai memberlakukan soal dengan daya nalar tingkat tinggi atau HOTS (High Order Thinking Skills) pada soal Ujian Nasional (UN). Dan karena itulah soal UN SMA 2018 yang telah dilaksanakan pada Selasa, 10 April 2018 ini menuai banyak kontroversi karena dianggap jauh berbeda dari kisi-kisi yang telah diberikan sebelumnya, mengingat 10% dari soal tersebut adalah soal HOTS. ya sudahlah baik soal lebih mudah maupun lebih sulit jika adik-adik tidak belajar tetap sulit dalam mengerjakannya, dengan itu kami semua mensuport adik-adik semua untuk semangat dalam belajar dan mempersiapkan segala sesuatunya dalam mengikuti berbagai rangkaian Ujian Nasional Tahun 2019. Terutama jaga kesehatan yah adik-adik jangan sampai setiap hari belajar larut malam lupa istirahat dan konsumsi makanan yang sehat malah sakit saat Ujian Nasional. itu jangan sampai terjadi, jadi tips sukses mengikuti Ujian Nasional adala Berdo'a, Ikhtiar Belajar dan yang tidak kalah penting adalah menjaga kesehata.
Baik langsung saja saya akan membagikan Soal dan Pembahasan UNBK Matematika SMA IPA 2018
1. Jika a.
b.
c.
d.
e. 3
Selesaian:
Ingat bahwa
=
Ingat bahwa
=
=
=
Ingat sifat logaritma :
=
=
Pada umunya di logaritma, basis 10 tidak perlu dituliskan, maka
Dengan menggunakan sifat logaritma, 1 juga dapat diubah menjadi bentuk
Sehingga
Ingat sifat
Jadi
2. Diketahui
a. 4
b. 2
c. 1
d. -2
e. -4
Selesaian:
Ingat bahwa
Maka
Jadi
5. Batasan nilai m dari persamaan kuadrat
a.
b.
c.
d.
e.
Selesaian:
Ingat kembali bahwa suatu persamaan mempunyai:
- Akar real berbeda jika D > 0
- Akar real kembar jika D = 0
- Akar tidakreal jika D < 0
Syarat :
Jadi agar
7. Keliling sebuah persegipanjang 28 cm. sedang panjangnya 2 cm lebih panjang dari lebarnya. Luas dari persegipanjang adalah …
a.
b.
c.
d.
e.
Selesaian:
Misalkan:
- Ukuran keliling persegi panjang = K.
Diketahui bahwa Keliling persegipanjang = K = 28 cm
- Ukuran panjang persegi panjang = p.
- Ukuran lebar persegi panjang = l.
Diketahui 
Ingat bahwa ukuran keliling persegi panjang =Karena
Luas daerah persegipanjang =
Jadi Luas daerah persegipanjang tersebut adalah
12. Diketahui suku ke-3 dan suku ke-7 suatu barisan aritmetika berturut-turut adalah 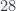 dan
dan  . Jumlah
. Jumlah  suku pertama deret tersebut?
suku pertama deret tersebut?
A. 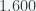
B. 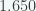
C. 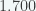
D. 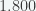
E. 
Untuk Soal UNBK Matematika Lainnya yang lebih lengkap bisa di lihat di bawah ini.
Untuk Soal UNBK Matematika Lainnya yang lebih lengkap bisa di lihat di bawah ini.
DemikianlahSoal dan Pembahasan UNBK Matematika SMA IPA 2018, Semoga Bermanfaat.
Source : m4th-labnet


0 komentar:
Posting Komentar